Combination of Resistors

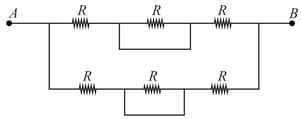
(i) Calculate the equivalent resistance of the given electrical network between points $A$ and $B$.

(ii) Also calculate the current through $CD$, if a $10 \mathrm{V} DC$ source is connected between $A$ and $B$, and the value of $R$ is assumed as  $2\Omega$.

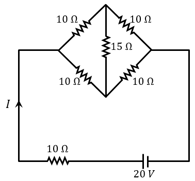
In the circuit, shown in the figure, the ammeter reading is

A wire is broken in four equal parts. A packet is formed by keeping the four wires together. The resistance of the packet in comparison to the resistance of the wire will be

The equivalent resistance of the network shown in figure between$A$and $B$ is 

The current $I$ in the circuit is

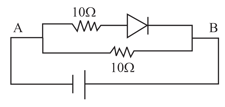
For the following circuit, the potential difference between x and y is

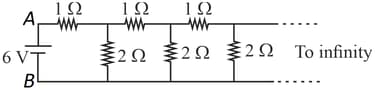
An infinite ladder network of resistances is constructed with $1\mathrm{ }\mathrm{\Omega }$ and $2\mathrm{ }\mathrm{\Omega }$ resistances. The $6\mathrm{ }\mathrm{V}$ battery between $A$ and $B$ has negligible internal resistance. The equivalent resistance between $A$ and $B$ is

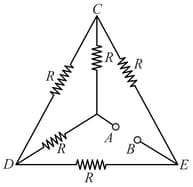
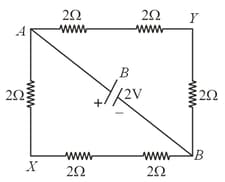
Consider the figure shown below. The resistance of the arrangement between the terminals $A$ and $B$ is:

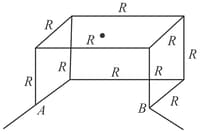
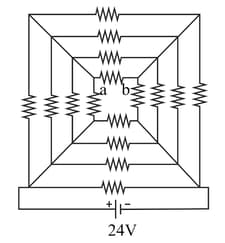
The figure shows  a circuit in which sixteen resistors each of resistance $5 \mathrm{\Omega }$ are connected to a battery of emf$24 \mathrm{V}$ . The current in  branch $ab$ is

'$n$' identical resistors are taken. '$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$' resistors are connected in series and the remaining are connected in parallel. The series  connected group is kept in the left gap of a meter bridge and the parallel connected group in the right gap. The distance of  the balance point in cm from the left end of the wire is
 

Twelve wires each of resistance $r$ ohm are connected in the form of a skeleton cube. Find the equivalent resistance of the cube when a cell is connected across any one of the wires forming the cube.

The effective resistance between points $A$ and $B$ of the network shown in figure is

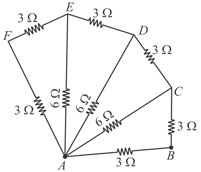
The equivalent resistance between points $A$ and $B$ with switch $S$ open and with switch $S$ closed are respectively.

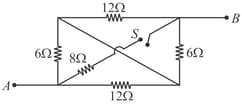
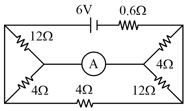
The potential difference across $4\mathrm{\Omega }$ resistor is,

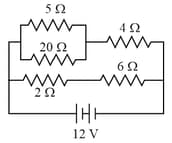
Find the equivalent resistance between $A$ and $B$.

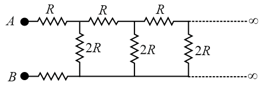
The equivalent resistance between points A and B in the circuit shown in the figure is,

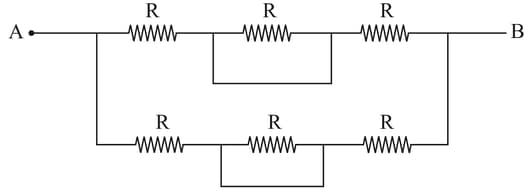
Find equivalent resistance across point $A$ and $B$

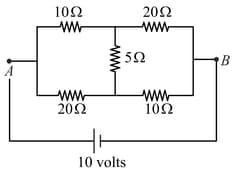
The equivalent resistance between points $A$ and $B$ in the circuit shown in the figure is: